REGRESIÓN MÚLTIPLE

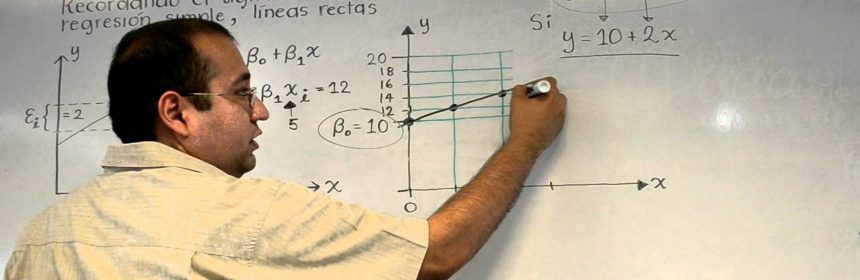
Utilizamos la regresión múltiple cuando estudiamos la posible relación entre varias variables independientes (predictorias o explicativas) y otra variable dependiente (criterio, explicada, respuesta).

Por ejemplo, podemos estudiar la inteligencia humana tomando el IQ como variable respuesta, y es posible que consideremos que puede estar relacionado con otras variables como: el tamaño del cerebro, el tamaño de la persona y su sexo. Podríamos añadirlas al estudio como variables independientes. Un modelo de regresión múltiple podría ofrecer una respuesta del tipo:

IQ = 80 + 0.02 Volumen cerebro + 0.15 Tamaño – 0.8 Sexo,

donde la variable sexo es una variable dicotómica o indicadora, codificada como 0 para las mujeres y 1 para los hombres. Para interpretar un modelo así hay que ser muy cautelosos. Los modelos de regresión múltiple nos informan de la presencia de relaciones, pero no de su mecanismo causal.

Otra fuente de problemas de interpretación es la relación entre variables independientes o colinealidad. Por ejemplo, el sexo puede parecer influir en la inteligencia según la ecuación, pero hay que considerar que las mujeres son habitualmente más pequeñas que los hombres. Si observamos los signos, apreciamos que compensa el efecto de una con la otra.

APLICACIONES DE LA REGRESIÓN MÚLTIPLE

La regresión múltiple se utiliza para la predicción de respuestas a partir de variables explicativas. Pero no es ésta realmente su aplicación más común en investigación. Sus usos más comunes son los siguientes:

• Identificación de variables explicativas. Nos ayuda a crear un modelo donde se seleccionen las variables que puedan influir en la respuesta, descartando las que no aporten información.
• Detección de interacciones entre variables independientes que afectan a la variable respuesta.
• Identificación de variables confusoras. Aunque es un problema difícil, es de interés en investigación no experimental.

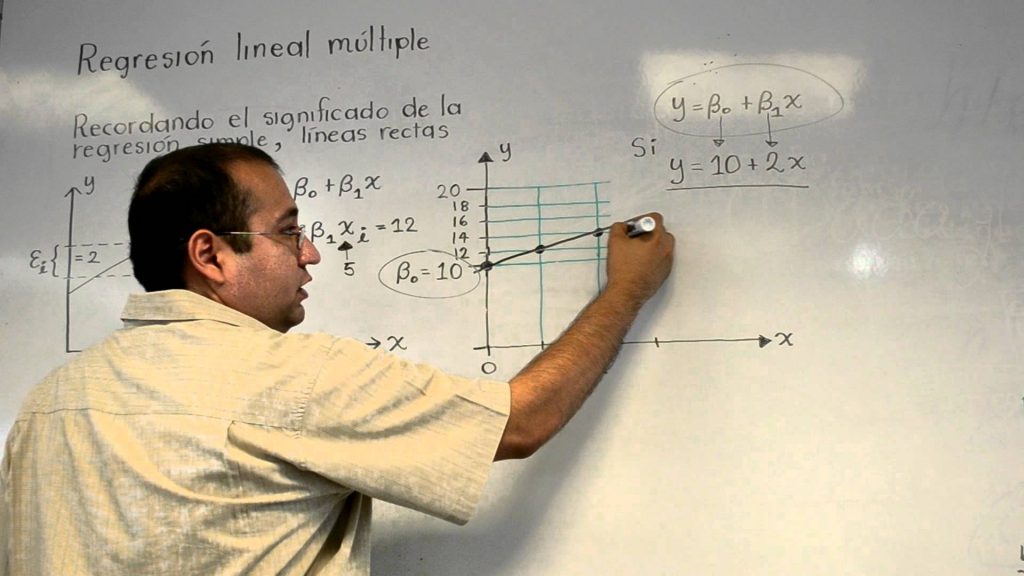
REQUISITOS Y LIMITACIONES DE LA REGRESIÓN MÚLTIPLE

Existen ciertos requerimientos necesarios para poder utilizar la técnica de regresión múltiple:

Linealidad: Se supone que la variable respuesta depende linealmente de las variables explicativas. Si la respuesta no aparenta ser lineal, debemos introducir en el modelo componentes no lineales.

Normalidad y equidistribución de los residuos: Para tener un buen modelo de regresión múltiple no es suficiente con que los residuos sean pequeños. La validez del modelo requiere que se distribuyan de modo normal y con la misma dispersión para cada combinación de valores de las variables independientes.

Número de variables independientes: Una regla que se suele recomendar es la de incluir al menos 20 observaciones por cada variable independiente que estimemos a priori interesantes en el modelo. Números inferiores nos llevarán posiblemente a no poder obtener conclusiones y errores de tipo II.

Colinealidad: Si dos variables independientes están estrechamente relacionadas y ambas son incluidas en un modelo, muy posiblemente ninguna de las dos sea considerada significativa, aunque si hubiésemos incluido sólo una de ellas, sí. Una técnica muy simple para detectar la colinealidad consiste en examinar los coeficientes del modelo para ver si se vuelven inestables al introducir la nueva variable.

Observaciones anómalas: Debemos poner especial cuidado en identificarlas y descartarlas si procede, pues tienen gran influencia en el resultado. A veces, son sólo errores en la entrada de datos, pero de gran consecuencia en el análisis.